This is part 4 of the Flare-On 5 CTF writeup series.
6 - Magic
The challenge starts with a humorous intro.
Wow you are a really good reverse engineer! Keep it up! You can do it!
How to tell if your child is a computer hacker:
1. They are using Lunix, an illegal hacker operating system
2. Are they struggling to maintain contact with the outside world, due to spending their time reading gibberish on the computer screen
This means this is a Lunix challenge, ahem, I mean Linux. The binary for our purpose is an x86-64 ELF. Let's give it a run.
$ ./magic
Welcome to the ever changing magic mushroom!
666 trials lie ahead of you!
Challenge 1/666. Enter key: abcdefghijkl
No soup for you!
Fair enough. The binary asks us for a key which we have no idea at present. But what about those 666 trials, do we really need to input 666 keys? Let's have a look in IDA.
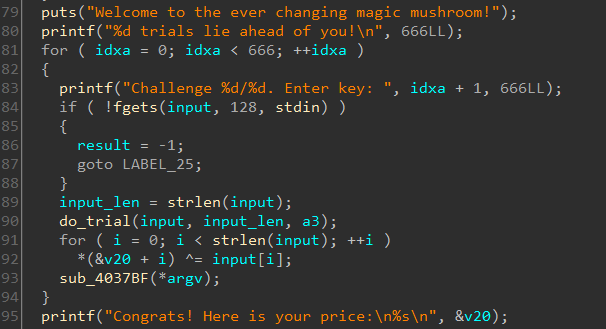
fgets read in the key which can have a max length of 128 bytes. do_trial checks our key.
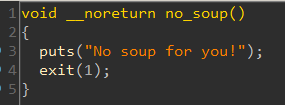
If our key doesn't match, it calls no_soup which terminates the program.
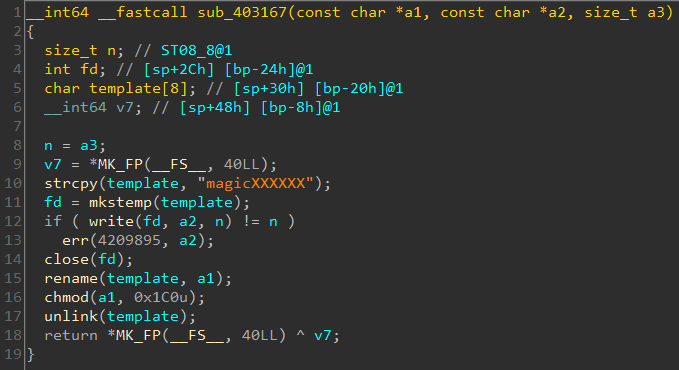
Going back to main there's a call to sub_4073BF right after do_trial which will only be called if our level key is correct. sub_4073BF calls some other function sub_403167.
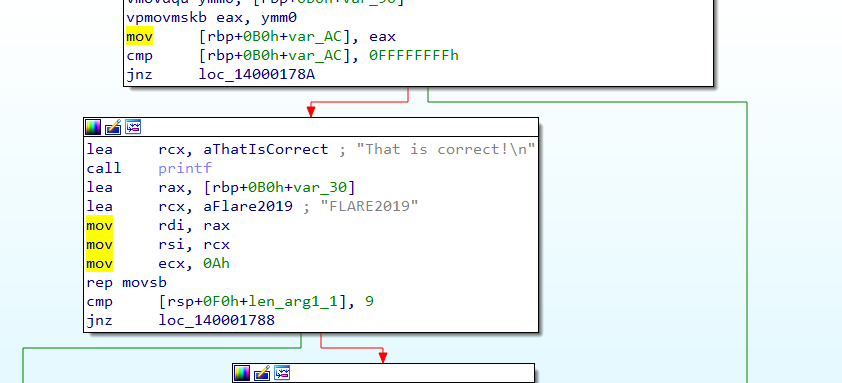
Going through the disassembly we can see it creates a temporary file. Some data is written to it and then renamed. We all look at it later. Let's focus on do_trial for now.
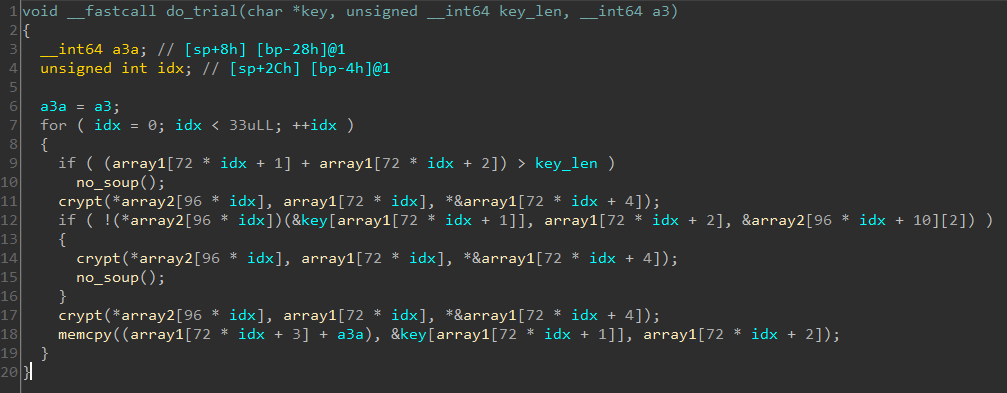
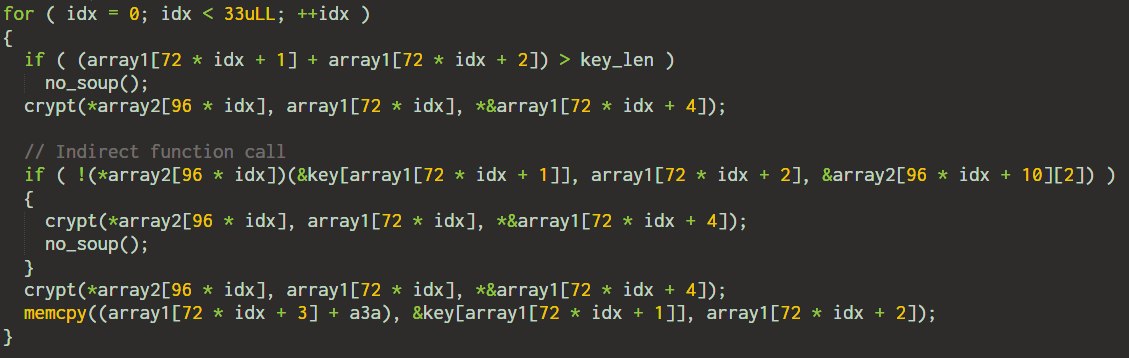
There's a loop which is run 33 times. In each iteration, the failure function no_soup will be called if -
- If the sum of the corresponding elements of
array1is greater than the key length. - The indirect function call inside the
ifstatement returns 0.
Condition 1 can be satisfied by providing a sufficiently long key close to 128 characters. Satisfying the condition requires finding the correct characters at the corresponding position.
Recovering the key check algorithms
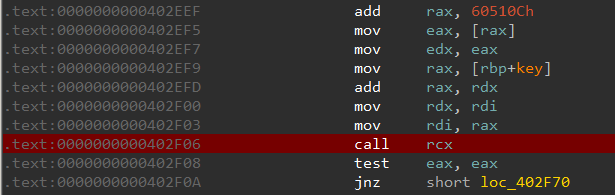
Let's debug this binary to know the target of the indirect call. Set a breakpoint at 402F06 which corresponds to the indirect function call.
When the breakpoint is hit, let us step into it. The call target is sub_400C55.
1. nth Fibonacci term
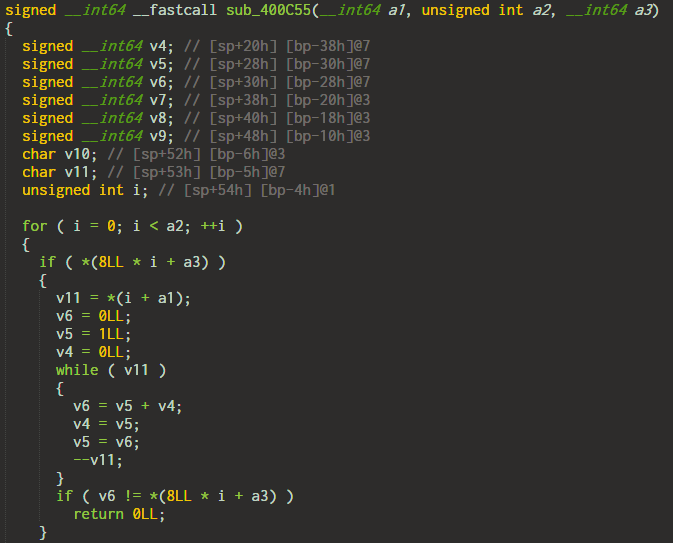
Decompiling this function we get the following code.
The function takes in 3 parameters where a1 and a3 are pointers to an array. a1 points to a character in the input array. a3 points to target array. After calculation on the input, this must match with the element in the target array. a2 is the number of sequential characters to check.
The code is very similar to how Fibonacci numbers are calculated. In fact, it is calculating the nth Fibonacci number where n is the ASCII value of the input character. For success, the calculated value must match with the corresponding element in a3. We can easily brute-force the correct values.
To keep the post short and readable, I will skip the details and won't show the debugging process where we can find the values in a1 and a3. But this is easy to find by setting a breakpoint at the appropriate location.
At the first run, the ASCII value of the three characters from position 2 (zero-based) is used to calculate the nth Fibonacci number. This must equal [0x12062F76909038C5, 0xEC9B9E4287BCE2D, 0x000000000035C7E2] for success. Bruteforcing, we get 'ds ' (quotes excluded) which matches with the target array. The Bruteforcer code will be presented shortly.
At each run of do_trial a different function checks for the correctness of the characters in out input key. Till now we have just seen the Fibonacci code. In total there are 7 different type of checking Functions.
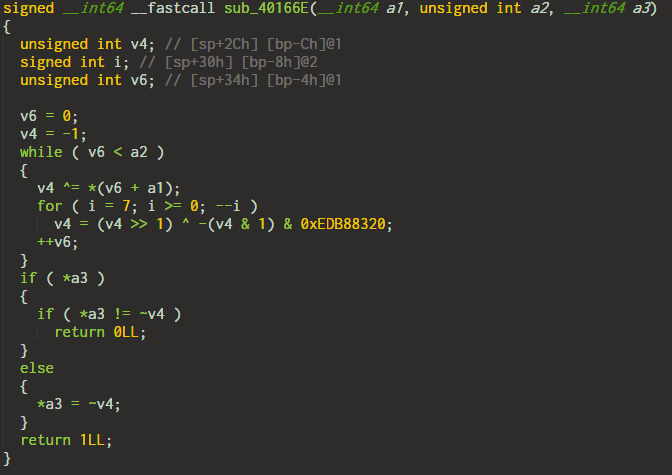
2. A sort of checksum function
This calculates a hash of the characters and compares it with a3.
3. XOR with a table
A table of values is generated. The characters of the input key are then xored. The details of the algorithm are skipped for brevity.
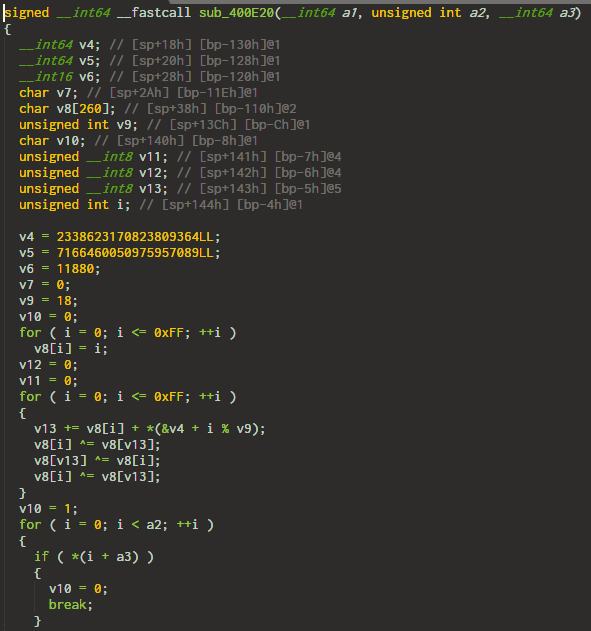
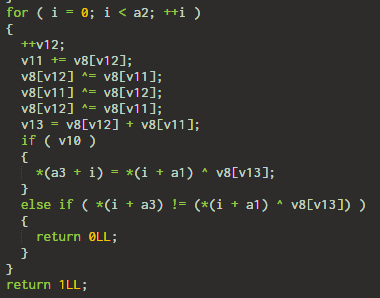
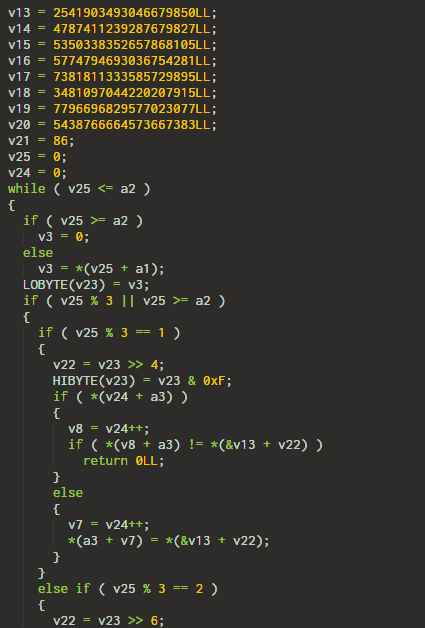
4. An unknown algorithm
I didn't need to figure out what the function was doing. The only thing worth noting the function must return 1. There is only a single line where the function returns 1 - the last line.
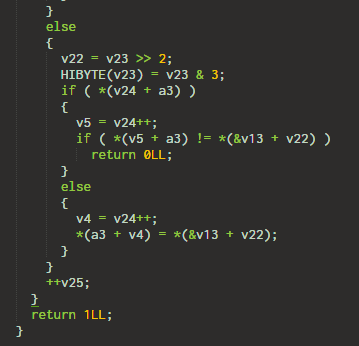
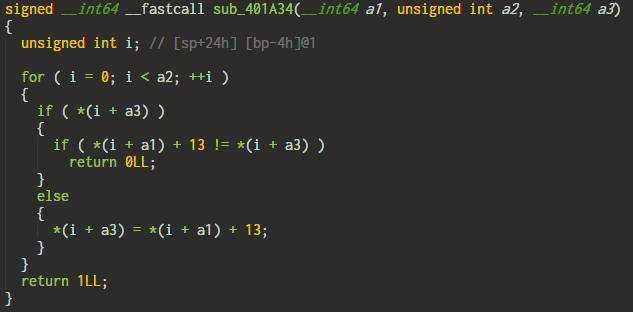
5. Plus 13
This simply adds 13 to the input character and compares it with the target.
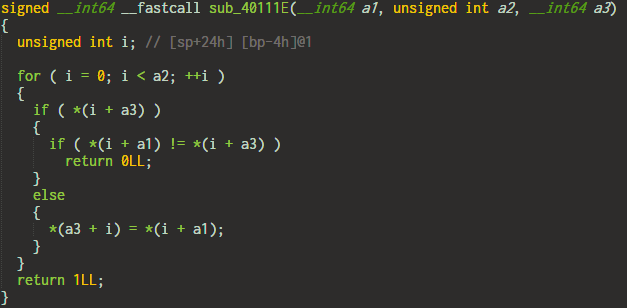
6. Equals
This is the simplest. It just compares input character with target as-is.
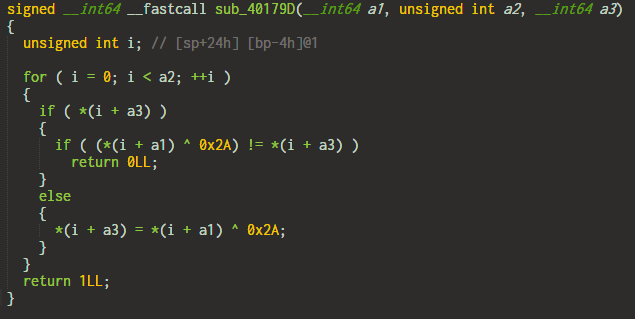
7. XOR with 0x2a
Input char is xored with 0x2a and compared with the target.
Recall that there was a function which wrote some data to a temporary file. The function would only be called if we were able to successfully find the level key. The purpose of the function was to modify the challenge file itself. The next time we run the challenge binary, the order of the in which the checking functions are called would be randomized. Hence it is important to replace the challenge binary with the original after every unsuccessful attempt or we run the risk of facing a moving target.
There're 666 levels in total. For each level, the key was checked using the above functions in some order. We do not fancy solving 666 levels by hand. We need to automate the process.
Automating the solving process
For each level, the checking functions were called in some order which we don't know beforehand. We need to devise a method such that it can identify the type of function being called and apply the corresponding technique to solve it.
Taking a hash of the function bytes seem to be a good choice. After all, the function addresses may vary but not the content of the function themselves. After dumping all seven different type of checking functions the minimal size in bytes was found to be 124. This means taking the hash of the first 124 bytes was enough. We can compare this hash to a list and call the corresponding solver automatically.
For this, I used radare2 to debug the binary. The binary requires input from stdin. This can be done by setting up a rarun2 dbg.profile.
stdout=/dev/pts/5
stdin=./input.txt
input.txt contains 666 lines filled with garbage characters. This will serve as a placeholder for feeding the fgets buffer.
r2-solver.py
The code for the solver is as follows
#r2-solver.py
import r2pipe
import os
import get_solver
import time
r2 = r2pipe.open('./magic')
r2.cmd('e dbg.profile=./dbg.rr2')
r2.cmd('doo')
# .text:0000000000402F03 mov rdi, rax
# .text:0000000000402F06 call rcx
# .text:0000000000402F08 test eax, eax
r2.cmd('db 0x402F06')
r2.cmd('db 0x402F08')
max_buffer_address = 0
for j in xrange(666):
print '[*] Trial %d--------------------' %(j+1)
for i in xrange(33):
# Continue
r2.cmd('dc')
# Now we are at 402F06 call rcx
solver = get_solver.get_solver(r2)
result = solver(r2)
print '[+] Solver output', ''.join(map(chr, result))
input_buffer = r2.cmdj('drj rdi')['rdi']
max_buffer_address = max(max_buffer_address, input_buffer + len(result))
#write result to input buffer
formatted_value = ''.join(map(lambda t:format(t,'x'), result))
r2.cmd('wx {} @rdi'.format(formatted_value))
# Continue
r2.cmd('dc')
# Now we are at 402F08 test eax, eax
r_rax = r2.cmdj('drj rax')['rax']
assert r_rax == 1
if i == 32:
r2.cmd('wx 00 @{}'.format(max_buffer_address))
time.sleep(0.1)
r2.cmd('dc')
time.sleep(1)
r2.quit()
os.system('chmod +rwx magic')
os.system('rm magic')
os.system('cp -f magic.bak magic')
os.system('chmod +rwx magic')
get_solver.py
get_solver.py calculates the hash of first 124 bytes of the function and calls the corresponding solver. The sign_array contains the md5 hashes.
#get_solver.py
import solver_cbmc
import solver_checksum
import solver_equals
import solver_fibo
import solver_plus13
import solver_tablexor
import solver_xor2a
import sys
def get_solver(r2):
# Calculate hash of first 124 bytes of function
hash_124b = r2.cmd('ph md5 124 @rcx')
sign_array = [
solver_cbmc.SIGN, solver_checksum.SIGN,
solver_equals.SIGN, solver_fibo.SIGN,
solver_plus13.SIGN, solver_tablexor.SIGN,
solver_xor2a.SIGN]
solver_fns = [
solver_cbmc.solve, solver_checksum.solve,
solver_equals.solve, solver_fibo.solve,
solver_plus13.solve, solver_tablexor.solve,
solver_xor2a.solve]
if hash_124b not in sign_array:
print '[!] No solver of sign {} found'.format(hash_124b)
print '[X] Bailing out...'
sys.exit(1)
return solver_fns[sign_array.index(hash_124b)]
Finally, let's have a look at the code for solvers.
1. Fibonacci solver
Straightforward. The nth Fibonacci number is given. Find n.
#solver_fibo.py
import struct
SIGN ='dc0c722a7bb7498ea259b8066dd20828'
def solve(r2):
print '[+] Running Fibonacci solver'
letter_count = r2.cmdj('drj')['rsi']
# Read quad words
buf = r2.cmd('p8 {} @rdx'.format(letter_count*8))
buf = buf.decode('hex')
fmt = '<{}Q'.format(letter_count)
target = struct.unpack(fmt, buf)
print '[+] Target ', target
soln = []
for t in target:
a=0
b=1
s=0
ctr=0
while True:
ctr += 1
s = a + b
s &= 0xFFFFFFFFFFFFFFFF
a = b
b = s
if s == t:
soln.append(ctr)
break
return soln
2. Checksum solver
We use the Z3 Theorem Prover to solve this.
#solver_checksum.py
import z3
import struct
SIGN = 'ac9c75e071087d1d234d51fcaaa8f70c'
def solve(r2):
print '[+] Running Checksum solver'
letter_count = r2.cmdj('drj')['rsi']
# Read single dword
buf = r2.cmd('p8 4 @rdx')
buf = buf.decode('hex')
target = struct.unpack('<L', buf)[0]
print '[+] Target ', target
i_vecs = [z3.BitVec('i{}'.format(i), 32) for i in xrange(letter_count)]
s = z3.Solver()
v4 = z3.BitVecVal(0xFFFFFFFF, 32)
for i in xrange(letter_count):
s.add(i_vecs[i] >= 22)
s.add(i_vecs[i] <= 126)
v4 ^= (i_vecs[i] & 0xFF)
j = 7
while j >= 0:
v4 = z3.LShR(v4, 1) ^ (-(v4 & 1)) & 0xEDB88320
j -= 1
s.add(target == ~v4)
assert s.check() == z3.sat
m = s.model()
soln = [m[v].as_long() for v in i_vecs]
return soln
3. Table XOR solver
We calculate the table and reverse the algorithm.
#solver_tablexor.py
import struct
SIGN = 'cff927fd6f27f0ed5a42ee3743b9513f'
table = [220, 72, 143, 86, 188, 54, 176, 100,
64, 39, 230, 44, 210, 63, 194, 52, 93, 82, 238,
205, 170, 202, 129, 141, 113, 35, 40, 215, 150,
78, 127, 107, 161, 62, 163, 18, 145, 38, 228, 3,
96, 140, 1, 68, 121, 227, 132, 53, 184, 74, 193,
85, 26, 157, 17, 231, 146, 164, 212, 104, 55, 133,
98, 102, 252, 191, 216, 152, 154, 142, 50, 32, 22,
56, 87, 14, 24, 91, 244, 23, 30, 160, 221, 83, 95,
6, 248, 246, 225, 12, 2, 116, 243, 192, 195, 240,
60, 148, 16, 219, 4, 249, 8, 214, 31, 190, 239,
149, 229, 80, 182, 171, 90, 25, 173, 36, 153, 67,
203, 165, 235, 57, 204, 103, 185, 197, 201, 166,
106, 144, 122, 15, 217, 59, 28, 232, 168, 126, 196,
114, 139, 99, 27, 89, 7, 73, 174, 5, 169, 236, 0,
198, 49, 20, 105, 186, 130, 29, 101, 70, 112, 41,
175, 200, 222, 208, 253, 119, 115, 43, 109, 223,
108, 254, 48, 47, 241, 120, 33, 124, 77, 206, 19,
181, 151, 42, 158, 255, 234, 207, 37, 189, 172, 76,
13, 128, 233, 178, 75, 250, 84, 65, 137, 58, 81,
247, 0, 138, 45, 218, 51, 242, 34, 155, 213, 162,
69, 110, 79, 211, 118, 61, 134, 46, 187, 123, 10,
66, 177, 94, 237, 156, 224, 136, 125, 21, 147, 209,
131, 111, 251, 180, 159, 71, 9, 167, 135, 245, 97,
226, 199, 179, 117, 11, 88, 92]
def solve(r2):
global table
print '[+] Running table xor solver'
letter_count = r2.cmdj('drj')['rsi']
# Read bytes
buf = r2.cmd('p8 {} @rdx'.format(letter_count))
buf = buf.decode('hex')
fmt = '<{}B'.format(letter_count)
target = struct.unpack(fmt, buf)
table_copy = table[:]
soln = []
v12 = 0
v11 = 0
for t in target:
v12 += 1
v12 &= 0xff
v11 += table_copy[v12];
v11 &= 0xff
table_copy[v12] ^= table_copy[v11]
table_copy[v11] ^= table_copy[v12]
table_copy[v12] ^= table_copy[v11]
v13 = table_copy[v12] + table_copy[v11]
v13 &= 0xff
soln.append(t^table_copy[v13])
return soln
4. The unknown algorithm solver
This was solved in the most interesting way. All we knew was that the function must return 1 which was at the last line in the decompiled code. We took the decompiled code from Hex-Rays and used the Bounded Model Checker (CBMC) tool from Carnegie Mellon. This tool is generally used to verify the correctness of C/C++ programs but can also be used as a SAT solver.
The idea was to tell CBMC that given the target array there is no such input which would make the function return 1. CBMC would then try to refute our claim by finding an input which made the function return 1. This is the answer we are after.
The C code fed to CBMC is as follows.
//solver_cbmc.c
unsigned char nondet_unsigned_char();
int solve()
{
#include "cbmc_clauses.h"
char v3; // al@3
int v4; // eax@8
int v5; // eax@9
int v7; // eax@13
int v8; // eax@14
int v9; // eax@18
int v10; // eax@19
int v11; // eax@23
int v12; // eax@24
//char v13[64]; // [sp+18h] [bp-50h]@1
unsigned char v14; // [sp+5Dh] [bp-Bh]@7
short v15; // [sp+5Eh] [bp-Ah]@5
int v16; // [sp+60h] [bp-8h]@1
unsigned int v17; // [sp+64h] [bp-4h]@1
char v13[] = {42, 57, 95, 100, 194, 167, 70, 35, 83, 107, 116, 71, 40, 77, 112, 66, 73, 37, 82, 106, 98, 56, 64, 74, 105, 69, 68, 89, 45, 49, 36, 80, 103, 121, 84, 33, 76, 118, 113, 102, 43, 99, 104, 109, 81, 87, 79, 48, 101, 78, 90, 52, 117, 110, 51, 108, 55, 72, 38, 50, 119, 97, 122, 75, 86, 0};
v17 = 0;
v16 = 0;
while ( v17 <= a2 )
{
if ( v17 >= a2 )
v3 = 0;
else
v3 = a1[v17];
// LOBYTE(v15) = v3;
v15 = (v15 & 0xFF00) | v3;
if ( v17 % 3 || v17 >= a2 )
{
if ( v17 % 3 == 1 )
{
v14 = v15 >> 4;
// HIBYTE(v15) = v15 & 0xF;
v15 = (v15 & 0xff) | ((v15 & 0xF) << 8);
if ( a3[v16] )
{
v8 = v16++;
if ( a3[v8] != v13[v14] )
return 0LL;
}
}
else if ( v17 % 3 == 2 )
{
v14 = v15 >> 6;
if ( a3[v16] )
{
v10 = v16++;
if ( a3[v10] != v13[v14] )
return 0LL;
}
if ( v17 < a2 )
{
v14 = v15 & 0x3F;
if ( a3[v16] )
{
v12 = v16++;
if ( a3[v12] != v13[v14] )
return 0LL;
}
}
// HIBYTE(v15) = 0;
v15 &= 0xFF;
}
}
else
{
v14 = (unsigned char)v15 >> 2;
// HIBYTE(v15) = v15 & 3;
v15 = (v15 & 0xFF) | ((v15 & 3) << 8);
if ( a3[v16] )
{
v5 = v16++;
if ( a3[v5] != v13[v14] )
return 0LL;
}
}
++v17;
}
__CPROVER_assert(0, "If we reach here, we found a solution!");
return 1;
}
The driver python program.
#solver_cbmc.py
import re
import struct
import commands
SIGN = '6b8cc66a8eec31e4272202f7b0ca8d4d'
def solve(r2):
print '[+] Running cbmc solver'
letter_count = r2.cmdj('drj')['rsi'] + 1
# Read bytes
buf = r2.cmd('p8 {} @rdx'.format(letter_count))
buf = buf.decode('hex')
fmt = '<{}B'.format(letter_count)
target = struct.unpack(fmt, buf)
print '[+] Target', target
f = open('cbmc_clauses.h', 'w')
for t in xrange(1, letter_count):
print >>f, 'unsigned char char%d = nondet_unsigned_char();' %t
print >>f, '__CPROVER_assume(char%d >= 22 && char%d <= 126);' %(t,t)
print >>f, "unsigned char a1[] = {",
print >>f, ','.join([" char%d" %i for i in xrange(1,letter_count)]),
print >>f, "};"
print >>f, "unsigned int a2=%d;" %(letter_count-1)
print >>f, "unsigned char a3[] = {",
print >>f, ','.join([" %d" %i for i in target]),
print >>f, "};"
f.close()
output = commands.getoutput('./cbmc solver_cbmc.c --trace --function solve --verbosity 4')
# means cbmc was able to find a solution
assert 'VERIFICATION FAILED' in output
soln = []
for t in xrange(1, letter_count):
val = int(re.search(r'char%d=([123456789]\d*)' %t, output).group(1))
soln.append(val)
return soln
5. Plus 13 solver
#solver_plus13.py
import struct
SIGN = '84545d65b725693a3c388be64b81502c'
def solve(r2):
print '[+] Running plus13 solver'
letter_count = r2.cmdj('drj')['rsi']
# Read bytes
buf = r2.cmd('p8 {} @rdx'.format(letter_count))
buf = buf.decode('hex')
fmt = '<{}B'.format(letter_count)
target = struct.unpack(fmt, buf)
soln = map(lambda t:t-13, target)
return soln
6. Equals solver
#solver_equals.py
import struct
SIGN = 'fd8f5d96b293b5779b1711f0dcdda8dd'
def solve(r2):
print '[+] Running equals solver'
letter_count = r2.cmdj('drj')['rsi']
# Read bytes
buf = r2.cmd('p8 {} @rdx'.format(letter_count))
buf = buf.decode('hex')
fmt = '<{}B'.format(letter_count)
target = struct.unpack(fmt, buf)
soln = target
return soln
7. XOR with 0x2a solver
#solver_xor2a.py
import struct
SIGN = '406aceb9202e9b1dc718cb09eb61c250'
def solve(r2):
print '[+] Running xor2a solver'
letter_count = r2.cmdj('drj')['rsi']
# Read bytes
buf = r2.cmd('p8 {} @rdx'.format(letter_count))
buf = buf.decode('hex')
fmt = '<{}B'.format(letter_count)
target = struct.unpack(fmt, buf)
soln = map(lambda t:t^0x2a, target)
return soln
Running r2-solver.py takes a couple of minutes and we finally are greeted with the flag.
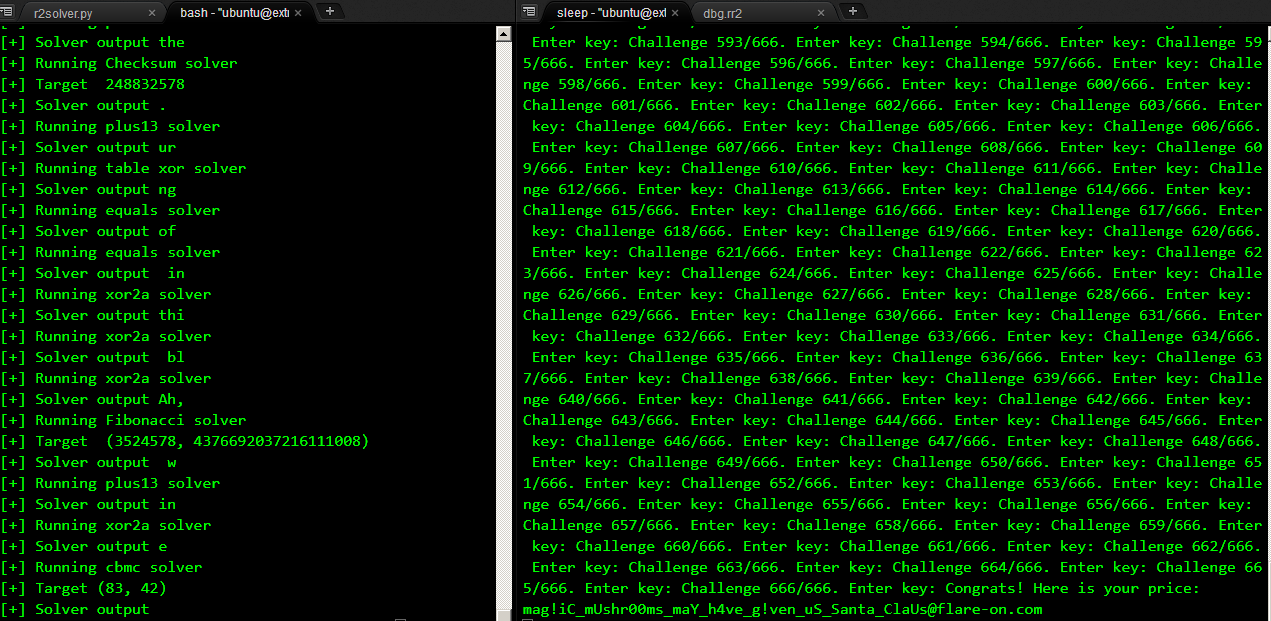
All 666 levels solved without breaking our keyboard!.
FLAG: mag!iC_mUshr00ms_maY_h4ve_g!ven_uS_Santa_ClaUs@flare-on.com
Continue to the next part: Flare-on 5 CTF Write-up (Part 5)